장음정, 단음정

장음정과 단음정을 구분하는 가장 쉬운 방법은 바로 '반음의 유무'이다.

두 음 사이에 반음이 있는지, 없는지에 따라 장음정인지, 단음정인지 알 수 있다.

두 음 사이가 온음으로 맞아떨어지면 반음이 없다고 표현하고,

온음으로 맞아떨어지지 않고 반음이 남으면 반음이 있다고 표현한다. (뒤에서 자세히 설명하겠다.)

또한 두 음정 사이가 장음정인 상태에서 반음만큼 가까워지면 단음정으로 변하고

단음정인 상태에서 반음만큼 멀어지면 장음정으로 변하게 된다는 것을 기억하도록 한다.

2도와 3도

: 두 음 사이에 반음이 있으면 단음정, 반음이 없으면 장음정이 된다.

2도

C와 D, E와 F는 모두 2도 음정이지만 C와 D는 온음, E와 F는 반음이다. 따라서 C와 D는 장 2도, E와 F는 단 2도가 되는 것이다.

누군가 설명을 읽고 온음은 반음이 2개니까 반음이 더 많은 거 아닌가? 하는 의문을 품을 수 있다.

하지만 큰 단위를 먼저 사용하는 것이 원칙이므로 두 음정 사이의 거리를 계산할 때도 온음을 우선적으로 사용하여 계산해야 한다.

임시표가 붙은 경우도 살펴보자

C와 Db의 경우 임시표를 제외하고 도수를 확인했을 때 장 2도라는 것을 알 수 있다.

하지만 위에 음인 D에 b이 붙으면서 두 음 사이가 가까워졌기 때문에 단 2도로 바뀐다.

두 번째 예로 E와 Eb은 몇 도일까?

임시표를 제외하고 도수를 확인해보자. E와 E 두 음정은 2도가 아니라 1도라는 것을 확인할 수 있다.

E와 Eb은 반음으로 단 2도와 같은 거리이지만 도수가 1도이기 때문에 단 2도가 될 수 없다.

두 음 사이가 반음이라고 해서 무조건 단 2도가 아니며 온음이라고 해서 무조건 장 2도가 아닌 것이다. 이는 모든 음정에서 똑같이 적용된다. 때문에 먼저 임시표를 제외한 두 음이

1. 몇 도인지

2. 장음정인지 단음정인지 확인 후

3. 임시표에 의해 가까워졌는지, 멀어졌는지 확인해야 한다.

3도

마찬가지이다.

C와 E 사이에는 반음이 없으므로 장 3도, A와 C 사이에는 반음(B와 C)이 있으므로 단 3도가 된다.

임시표가 붙은 경우도 살펴보자

C와 Eb일 경우 임시표를 제외하고 도수를 먼저 확인해보면 장 3도라는 걸 알 수 있다.

하지만 E에 b이 붙으면서 두 음 사이가 가까워졌다. 따라서 C와 Eb은 단 3도인 것이다.

마찬가지로 Bb과 D는 임시표 제외하고 도수를 따졌을 때 단 3도이다. 하지만 밑에음(B)에 b이 붙으면서 두 음 사이가 멀어졌기 때문에 장 3도가 된다.

위에서 예시를 든 것처럼 F와 G#은 단 3도와 음의 거리는 같지만 도수가 2도이기 때문에 단 3도가 아니다.

6도와 7도

: 두 음 사이에 반음이 있으면 장음정, 반음이 없으면 단음정이 된다.

6도

C와 A, E와 C는 모두 6도이다. 하지만 C와 A사이에는 반음(E와 F)이 있기에 장 6도이고, E와 C 사이에는 반음이 없기에 단 6도이다.(두 음 사이에는 반음이 E와 F, B와 C로 2개가 존재한다. 하지만 반음이 2개인 경우, 합쳐서 온음이 되기 때문에 반음이 없다고 표현한다.)

임시표가 붙은 경우를 살펴보자.

먼저 C와 Ab의 경우 임시표를 제외한 C와 A는 장 6도이다. 하지만 위의 음(A)에 b이 붙으면서 두 음 사이가 가까워졌다. 따라서 C와 Ab은 단 6도가 된다.

B와 G#의 경우 임시표를 제외한 도수는 단 6도이지만 위의 음(G)에 #이 붙으면서 두 음 사이가 멀어졌다. 따라서 두 음은 장 6도가 된다.

7도

마지막으로 7도를 살펴보자.

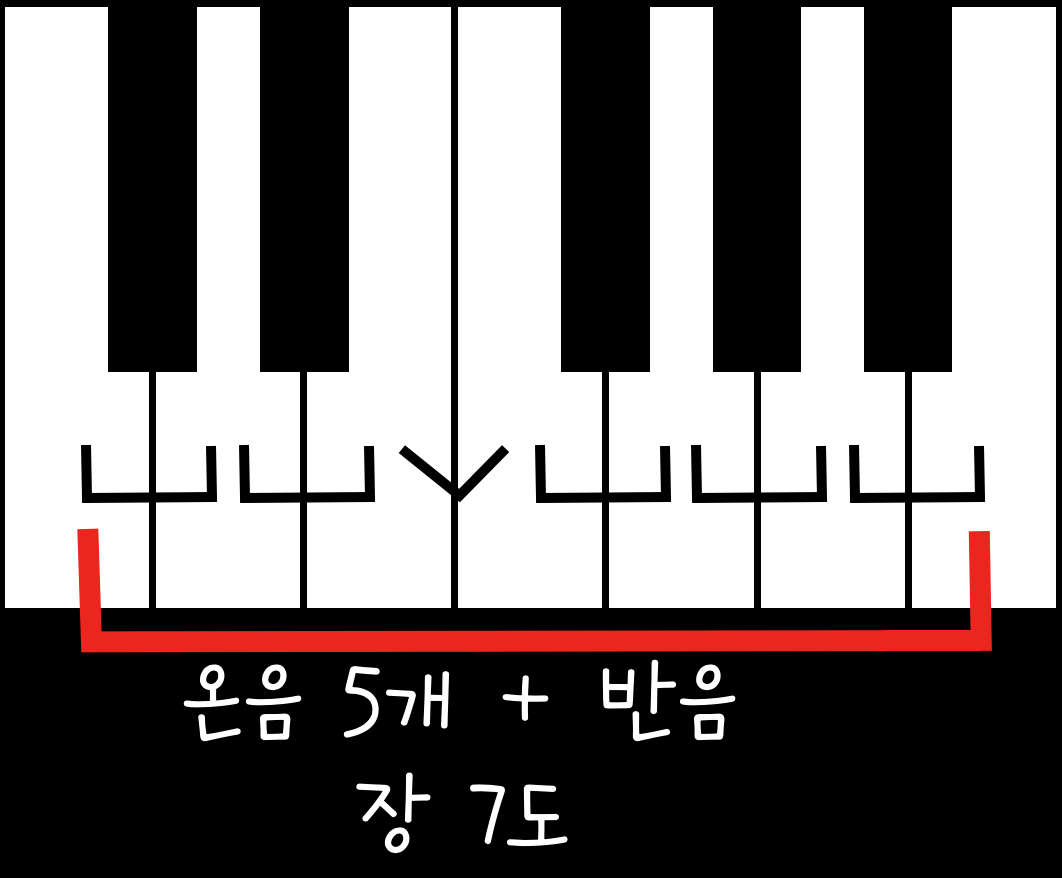
C와 B 사이에는 반음(E와 F)이 존재하기 때문에 장 7도, D와 C 사이에는 반음(E와 F, B와 C가 만나 온음으로 바뀜)이 없기 때문에 단 7도가 된다.

임시표가 붙은 경우를 살펴보자

C와 Bb는 임시표를 제외한 도수는 장 7도이다. 하지만 위의 음(B)에 b이 붙으면서 두 음이 가까워졌다. 따라서 단 7도가 된다.

Db과 C의 경우 임시표를 제외한 도수는 단 7도이지만 아래음(D)에 b이 붙으면서 두 음이 멀어졌다. 때문에 두 음은 장 7도가 된다.